Skeptic’s Play has a couple of interesting geometry puzzles I’ve repeated below:
Let’s say I’ve painted a plane — the flat kind, not the flying kind. Every single point on the plane is assigned the color red or blue. Prove that there must exist two points of the same color that are exactly one unit apart.
Every single point on the plane is assigned the color red, blue, or green. Prove that there must exist two points of the same color that are exactly one unit apart.
What makes this interesting is that you can’t assume anything about how a plane could be painted. Mathematically, there can be all sorts of ways one could color a plane that are literally unimaginable. For example, if you color all points with rational number Cartesian coordinates with red, then the entire plane is colored red and yet it is at the same time almost completely colorless. Fractals are another example, where you can imagine large scale structures, but it’s not really possible to imagine it with all the small scale structures repeating no matter how much you zoom in. To prove the above statements, one needs to use a method that would still apply no matter how bizarrely the plane is colored.
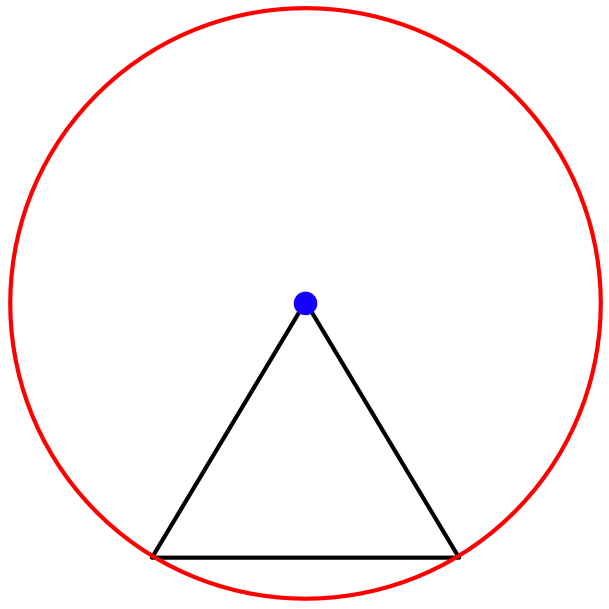
Anyways, the first statement is pretty easy to prove. Let’s assume that there are no two points that are one unit apart that have the same color. Then there are both red and blue points in the plane. If there was only one color , then any two points at unit distance would obviously be the same color. Let’s pick any blue point. Then the circle centered around the blue point with a unit radius must be completely red. Any two points on the circle that are a unit distance apart would both be red, which would be a contradiction.
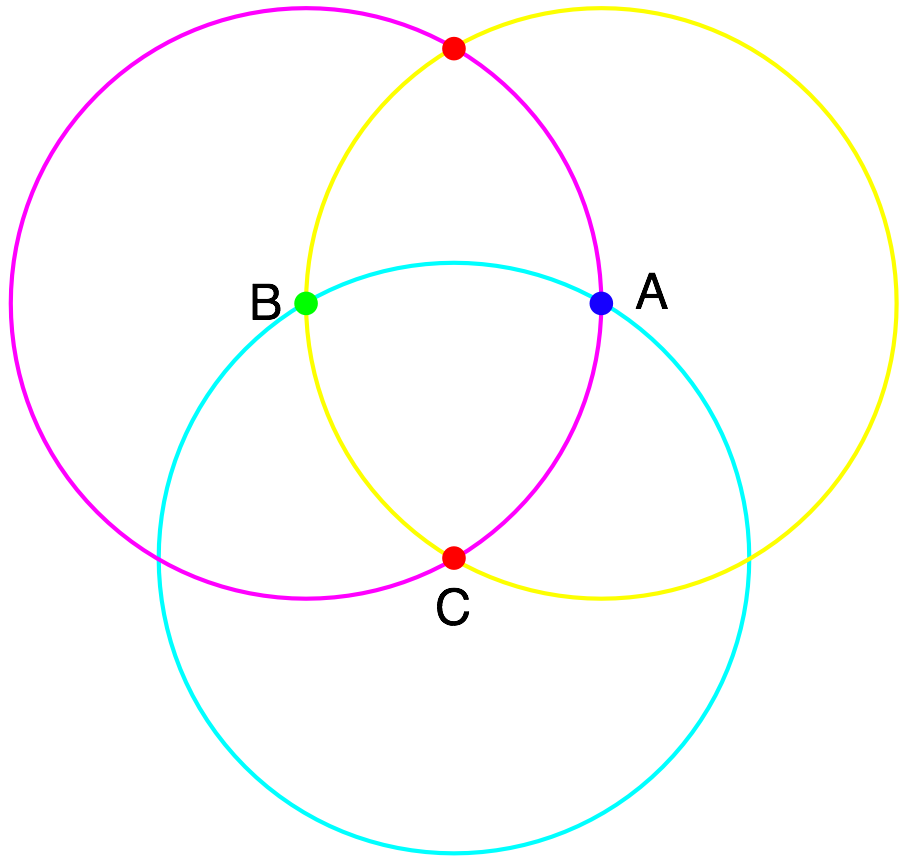
That was easy, but would the second statement be as easy to solve? Let’s try to repeat our approach and assume that no two points a unit distance apart has the same color. Without loss of generality, let’s pick any point A and say that it’s blue. Then the unit circle centered around A must be made of points that are either red or green. Again without loss of generality, let’s pick any point B on the circle and say that it’s green. Then the unit circle around B must be blue or red. Then point C at where the two circles intersect must be red. And the unit circle around C must be blue or green. I show this in the figure below, where a magenta circle is made up of points that can be either blue or red, a yellow circle is made up of points that can be either red or green, and a cyan circle is made up of points that can be either blue or green.
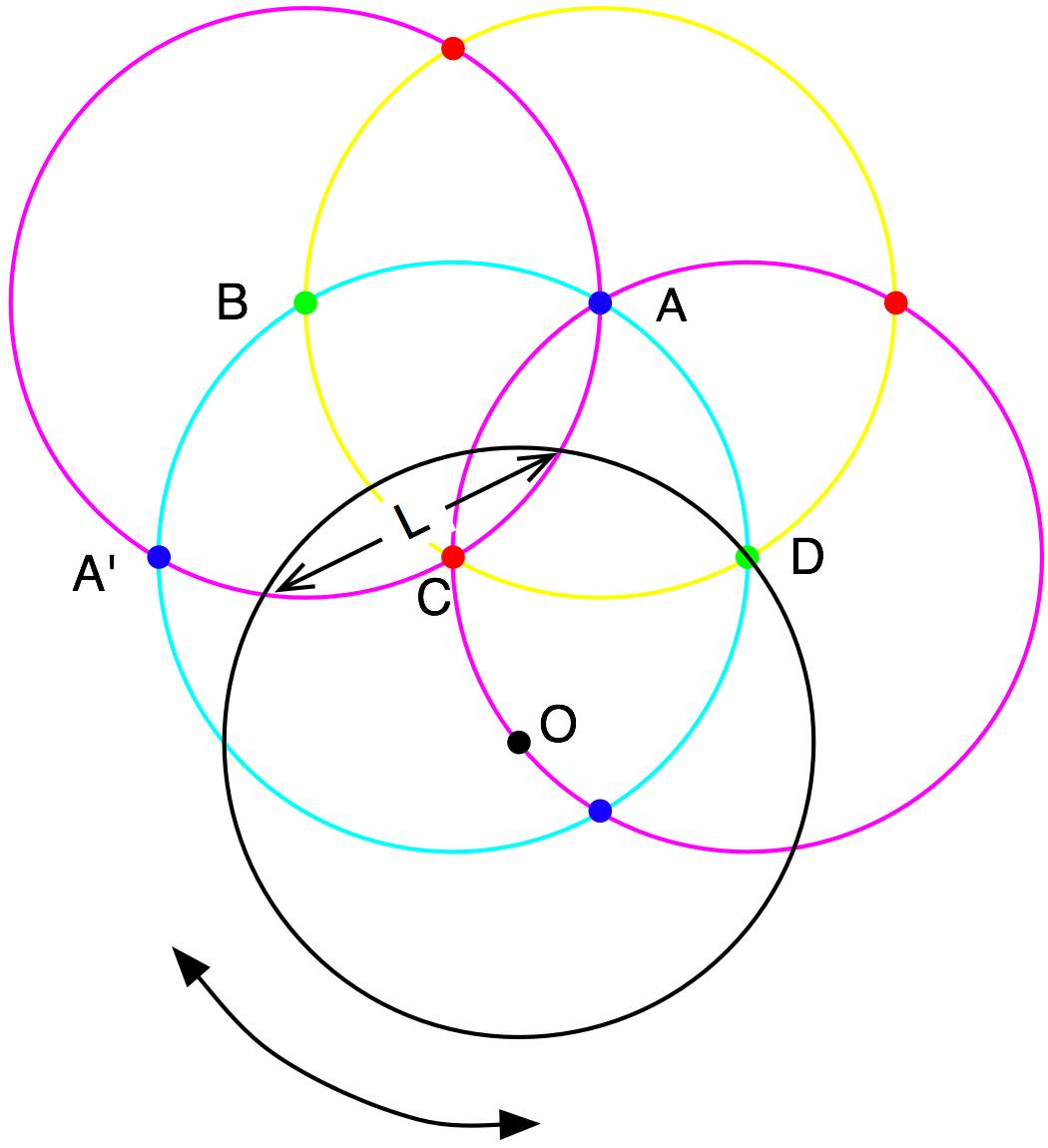
The obvious path to take is to repeatedly draw a circle around each intersection and hope there is a point which must result in a contradictory coloring. This would happen if magenta, yellow, and cyan circles all intersected at a single point. Unfortunately, this never happens no matter how far you go. In fact, we get a repeating pattern for the intersections that is consistent with our initial assumption. We need another approach.

Instead of trying to find two intersections from circles that are centered around existing intersections, we’ll try making a unit circle that isn’t centered around a pre-existing intersection. First we do what we did before until we get point D below. Then we move around a unit circle that passes through point D and the arc between A and A’ below. This unit circle must be centered around a point O on the magenta circle centered on D. We want to change L by moving point O and its circle around until it’s equal to the unit distance. This is possible since the smallest value for L is zero and the largest value is the square root of three or about 1.73, which is the distance between A and A’.
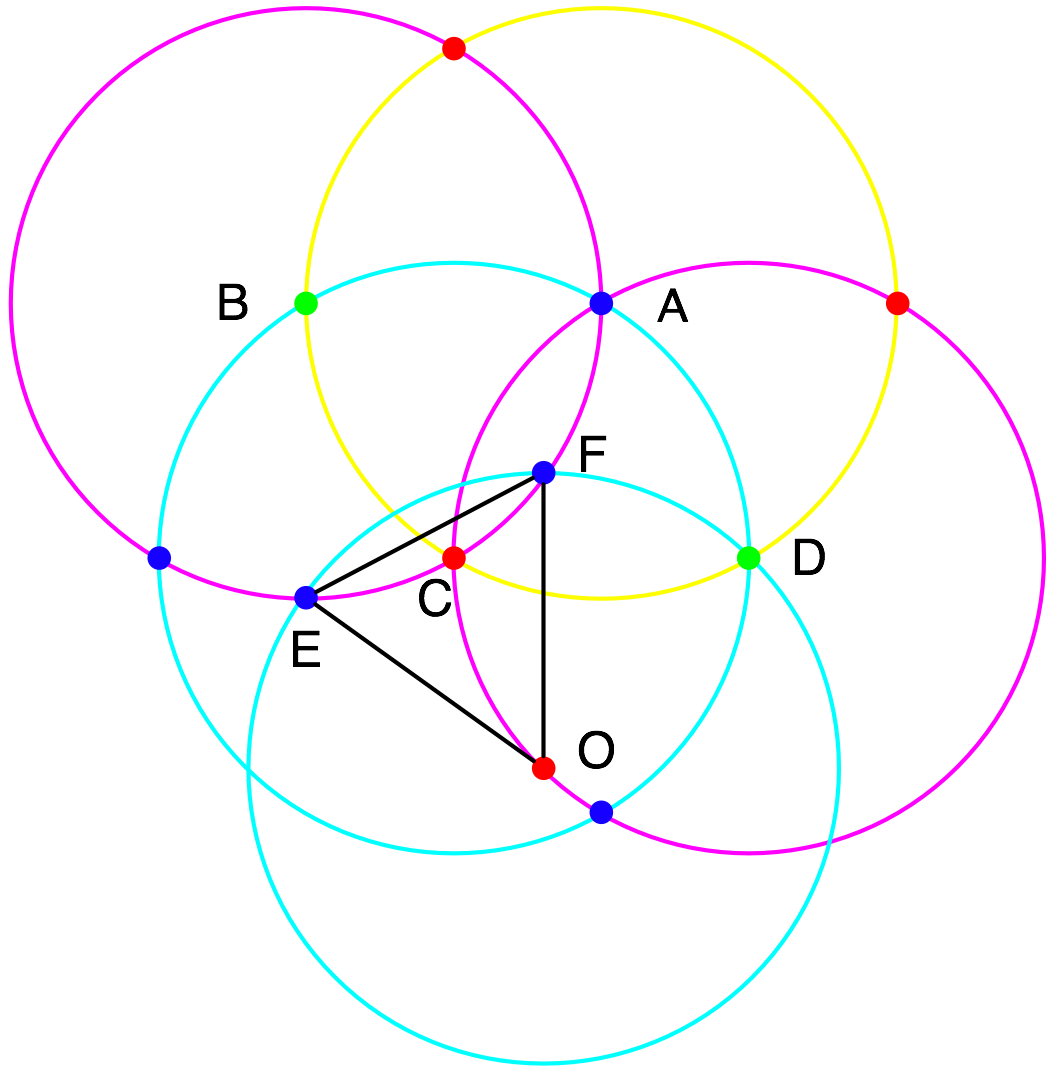
Once we move point O so that L becomes the unit distance as in below, we finally get our contradiction. Without loss of generality, assume that point O is colored red. Then points E and F, both being the intersection of the magenta and cyan circles, must both be blue. Since points E and F are a unit distance apart, this contradicts our initial assumption that no two points a unit distance apart are the same color.
This was a fun but frustrating puzzle to solve. Proving the first statement was really easy, but I got trapped in the dead-end approach for too long for the second statement. The ease of the first one kept me working on the second one since I thought it should also have a trivial solution. Unfortunately, I kept working with variations of the dead-end approach hoping to get an intersection with contradictory colorings, and it even reached the point that I wondered if there was a way to color a plane so that no two points a unit distance apart were the same color. But a slight detour in the approach helped me reach a simple solution, so I can now stop worrying about the puzzle.
It was a nice way to exercise my brain and prove that it hasn’t completely ossified yet. However, when the Skeptic’s Play gives its next puzzle, I should be wary of deceptively easy looking puzzles like this one, where the first half was so simple that it made me think the second half should also be as trivial. It should at least help prevent me from underestimating how much time I need to waste …